Over the course of the past week, I've had a lot of ideas come through my head that I haven't been able to incorporate into blog posts of their own. I'll try to put them out here, and hopefully some meaning can be derived from my ramblings :)

Nonlinearity

I've spoken before about this, but only in the context of time.

The world is highly nonlinear, both in the sense that it can't be predicted / extrapolated over any useful period of time, but also that life is very discrete. A small, continuous local change can show little visible impact for a while, until hitting a transition state, and altering completely its visible effect.

But a trap that so many people fall into is that of local linearity. Over a short enough timescale, with a sufficiently restricted perspective, life will look linear. Take school for example: Modern curriculum is built on the idea of learning as a "path", as something that can be systematically traversed from start to end, linearly, whereas knowledge takes the form more of a branching tree of topics.

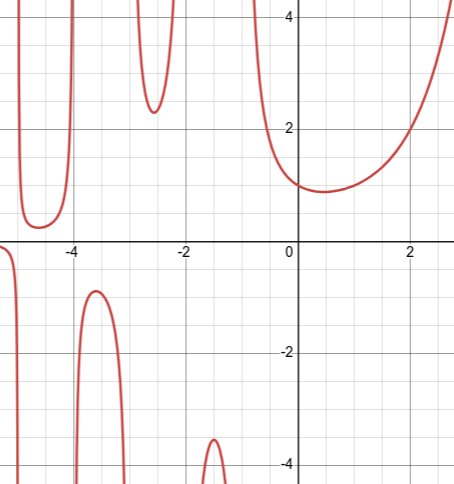
It's like looking at a small section of the gamma function, and concluding that it is a line:

where in reality, it's very irregular.

And so, what does this mean for decision making and the like?

In a linear system it is trivial to get from one point to another just by moving in a constant direction, but nonlinear is not so - to determine where an irregular function reaches a certain value, at the very least an algorithm that dynamically responds to changes is necessary.

State spaces

I like to think of a lot of things as state spaces. Take the example about school from earlier: knowledge itself is really a state space, too. Broad subjects like science or math or literature encompass large regions of this, whereas specific concepts nest into smaller and smaller sections. Within this model of state space, to really learn some concept means to understand all of the knowledge space contained by itself down to some resolution.

Resolution is another interesting property of state spaces - it is closely related to the lack of local linearity in such spaces.

In a way, the knowledge state space is fractal. Within each concept, there are further sub-concepts that build upon the first one, but these still are quite dissimilar from each other. This makes it locally nonlinear; zooming into a linear system only results in a progressively more uniform 'slice' of such system.

From this perspective, the linear system used in schools shows obivious flaws. It introduces topics as discrete chunks with seemingly clearly defined starts and ends, leaving little room for the infinite zoom that refines simpler, introductory topics into higher level ones. In fact, it does away with the nesting entirely: Classes like Calculus are thought of as different entities than the rest of the math classes that they build upon; constructs that begin and end totally separate from the foundation of algebra, geometry, trig, etc. that they build from.

How I've learned over most of my life has been to, in a way, map out the boundaries of whatever state space I am working with. That's why I spent so much of my elementary school reading about all sorts of science facts: I wanted to have some general idea about how the world worked, and I found it more efficient to throw enough random content into my brain to have an expansive, though low-resolution, map, which I could narrow down sections of if they interested me. (This is in a way like a breadth-first-search. depth-first-search does not work without a depth bound, but it is in essence a deep dive into one specific topic.)

Expansive mappings of state spaces, whether they be of knowledge or other things, I think are very useful because they enable, or at least make much easier to achieve the final construct I've been thinking about the past few days:

The End or the Beginning

What do you do when, following some question or train of thought, reach an "I don't know"?

I've seen too many people treat this as an end to the train of thought, as an answer to the question. But for me, the "I don't know" is only the beginning. Why don't I know? How can I know more?

In most cases, "I don't know" doesn't mean that one literally doesn't know anything about the problem at hand. There are almost always gradations; competition math & programming have taught me to break down larger problems into series of smaller observations which can be dealt with on their own.

But this where the representation of knowledge as discrete blocks is harmful - it makes understanding seem categorical into one of "learned, didn't learn, forgot", and without a system of nesting topics that might help one to derive specific concepts from the sum total of their neighbors.

Derivation is one of my favorite parts of learning. I've never enjoyed nor been good at memorizing masses of unrelated facts; I can only reliably remember interconnected systems. But also, I'm kind of lazy. In a lot of cases, especially with math, I try to get away with remembering only the method in which to obtain some conclusion so that I can avoid memorizing the actual fact itself. Furthermore, methods such as these are usually themselves easier to remember, because they are connected to more other concepts in the state space mapping than singular facts on their own. Connectivity is overall robust.

Curiosity overall I feel is a good thing to have - it drives us forward; makes us human. This sort of self-modification that we can do to ourselves is powerful if used right: rather than follow a linear path with constant direction, take control of your own direction.. in essence becoming a differential equation, so much more complex and varied than just a line.

and so the ramblings map back to themselves, a recurrence almost.. cyclical...

tags: life